Background¶
This section outlines the system being simulated as well as some theoretical background of learning mechanisms.
The system being simulated¶
Figure 1 illustrates the system being simulated.
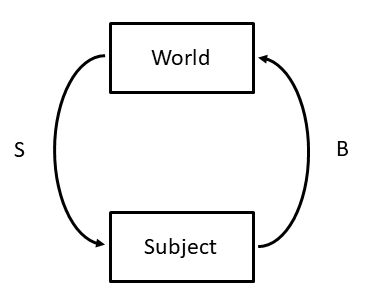
Figure 1: The world and the subject.¶
The system consists of a subject (or organism, individual, or agent) interacting with a world (or environment).
The world displays stimuli that the subject responds to. As a consequence of that response, the world displays the next stimulus, which the subject responds to. This continues, and the subject learns about the world in each step. The learning is modelled with a learning mechanism that uses a set of memory state variables to represent the subject’s memory of the past stimuli.
The subject has a pre-defined set of behaviors \(\mathscr{B}\) - the behavior repertoire. It also has an output function (decision function) that determines which of these behaviors to respond with. In addition, it has state transition functions that update memory state variables and other internal states.
The world, which often is defined by an experiment, has a pre-defined set of stimulus elements - the stimulus repertoire. It also has an output function that determines which of these stimuli to expose to the subject. In addition, it has state transition functions that update the state of the world. A stimulus \(S\) consists either of one single stimulus element \(S=\{E\}\) in the stimulus repertoire, or a set of two or more simultaneous elements \(S=\{E_1,E_2,\dotsc\}\). In the latter case, the stimulus is called a compound stimulus.
The behavior of the subject influences both the internal state of the subject and the internal state of the world. Also, the stimulus that the world generates depends on the subject’s behavior (being the response to the last generated stimulus), and the behavior that the subject responds with depends on the stimulus that it responds to.
The system operates in the discrete time steps \(S_{1}\rightarrow B_{1}\rightarrow S_{2}\rightarrow B_{2}\rightarrow S_{3}\rightarrow\dotsc\), in other words, the process starts with the world producing a stimulus \(S_1\) at time step 1, and the subject responds with behavior \(B_1\) at time step 2, etc. It is this process that is being simulated in Learning Simulator. The Learning Simulator scripting language specifies all the properties of the subject, the world and the simulation.
Technically, the world is a dynamical system whose state transition function depends on the subject’s last behavior, and outputs a stimulus. In the same way, the subject is a dynamical system whose state transition function depends on the last stimulus, and outputs a behavior. Thus, the system being simulated consists of two interacting dynamical systems.
The world¶
The world receives a behavior \(B\) from the subject and responds with a stimulus \(S\) that may or may not depend on \(B\). A description of the world specifies which stimulus is generated in each step and how it depends on the behavior and internal state variables of the world. In the Learning Simulator scripting language, this is done one or several @phase blocks of the script. It basically consists of a number of labelled lines, where each line specifies which stimulus to expose the subject to, and which line to go to in the next step.
The subject¶
When the subject interacts with the world, it learns about it. This learning, in other words, exactly how and which memory state variables are updated, is specified by a learning mechanism. The subject’s response to an observed stimulus is controlled by a decision function. This section describes the different learning mechanisms as well as the decision function.
The mechanisms¶
The subject is assumed to have an initial (genetic) value \(u_E\) for each stimulus element \(E\). The subject is also assumed to have a cost \(c_B\) associated with each behavior \(B\) in its behavior repertoire. These \(u\)- and \(c\)-values do not change during the simulation.
When the subject observes a stimulus \(S\) it makes a decision about which behavior \(B\) (in the behavior repertoire) to respond with. This is done by the decision function; see below.
The possible responses to a given stimulus \(S\) may be restricted to a subset of the subject’s behavior repertoire \(\mathscr{B}\). For example, if a stimulus involves a pressable lever, the subject can respond with the behavior “press lever”, but for a stimulus that does not involve a lever, the subject cannot respond with “press lever”. We use the notation \(\mathscr{B}(E)\) for the possible responses to the stimulus element \(E\), and \(\mathscr{B}(S)=\cup_{E\in S}\mathscr{B}(E)\) for \(S=\{E_1,E_2,\dotsc\}\). In the scripting language, such restrictions are specified in the parameter response_requirements.
After observing the next stimulus \(S'\) (being a consequence of the decision to respond with \(B\)), the subject “learns” by updating an internal state variable \(v\) indexed by stimulus-response pairs (so that \(v_{E\rightarrow B}\) is the value associated with the response \(B\) to stimulus element \(E\)). Some mechanisms also use a state variable \(w\) indexed by stimulus elements (so that \(w_E\) is the value associated with stimulus element \(E\)). The \(w\)-values are usually called conditioned reinforcement values. The table below shows the available learning mechanisms, their memory state variables, and how they are updated after the subject has experienced the steps
where \(S=\{E_1, E_2, \dotsc\}\) and \(S'=\{E'_1, E'_2, \dotsc\}\). In the table the following notation is used:
and
Mechanism |
Abbrev. |
Memory states |
Memory updates |
|
|---|---|---|---|---|
SR |
\(v_{E\to B}\) |
\(\Delta v_{E\to B}=\alpha_{E\to B}(u_{S'}-v_{S\to B}-c_B)\) |
\(\forall E\in S\) |
|
QL |
\(v_{E\to B}\) |
\(\Delta v_{E\to B}=\alpha_{E\to B}\big(u_{S'}-v_{S\to B}-c_B+\gamma\max\limits_{B'}v_{S'\to B'}\big)\) |
\(\forall E\in S\) |
|
Expected SARSA [5] |
ES |
\(v_{E\to B}\) |
\(\Delta v_{E\to B}=\alpha_{E\to B}\big(u_{S'}-v_{S\to B}-c_B+\gamma E(v_{S'\to B'})\big)\) |
\(\forall E\in S\) |
Actor-critic [6] |
AC |
\(v_{E\to B}\)
\(w_E\)
|
\(\Delta v_{E\to B}=\alpha_{E\to B}\beta_{E\to B}\big(1-\Pr(S\to B)\big)\delta\)
\(\Delta w_E=\alpha_E \delta\)
where \(\delta = u_{S'}+\gamma w_{S'}-w_{S}-c_B\)
|
\(\forall E\in S\) |
A-learning (Guided associative learning) [7] |
A, GA |
\(v_{E\to B}\)
\(w_E\)
|
\(\Delta v_{E\to B}=\alpha_{E\to B}(u_{S'}+\gamma w_{S'}-v_{S\to B})\)
\(\Delta w_{E}=\alpha_E (u_{S'}+\gamma w_{S'}-c_{B}-w_{S})\)
|
\(\forall E\in S\) |
Rescorla-Wagner |
RW |
\(v_{E_1\to E_2}\) |
Only implemented for single-element stimuli \(S=\{E\}\).
\(\Delta v_{E\to E'} = \alpha_{E\to E'}(\lambda_{E'}-v_{E\to E'})\)
\(\Delta v_{E\to X} = -\alpha_{E\to X} v_{E\to X} \; \forall X\ne E'\)
|
The decision function¶
When the subject is exposed to a stimulus \(S=\{E_1,E_2,\dotsc\}\), it makes a decision about which behavior in the
behavior repertoire to respond with. This is done by associating each possible behavior \(B_i\)
with a probability \(\Pr(S\rightarrow B_i)\) and then choosing a response by sampling from
this probability distribution. In
Learning Simulator a version of the so called soft-max rule is used to compute the probabilities:
where the parameters \(\beta_{E\to B}\) control the extent to which the decision is governed by the \(v\)-values: Smaller \(\beta\) means more exploration in the reponse decision. The parameter \(\mu\) may be used for genetic predisposition, for example to increase/decrease the probability for a particular response to a particular stimulus element.
References